This article is excerpted from The Audio Expert by Ethan Winer. You can read more about this book at Ethan’s web site: http://ethanwiner.com/book.htm
For bowed instruments such as violins and cellos, their tone quality, or timbre, is affected by where on the string the bow is placed, how hard it’s pressed against the string, and how quickly it’s drawn across the string. These three parameters vary the timbre through its entire range of possibilities. Here, timbre describes the relative volumes of the fundamental pitch and its many harmonic multiples.
With wind instruments, the shape of your lips and mouth, and how hard you blow, determines the timbre. Blowing harder creates harmonics that are louder than when blowing with less force. The same applies to plucked instruments such as the guitar or banjo - striking the string harder, or nearer to one end, creates stronger harmonic content. The same principle applies to acoustic instruments. The harder you blow a trumpet or oboe, or strike a drum, the brighter the sound will be. Drum overtones also vary in level depending on where you strike them and how hard. Striking a drum near the edge makes overtones louder relative to the fundamental, compared to striking it near the center. This applies to pretty much every other acoustic sound source that occurs in nature.
Many people don’t realize that learning to control the bow is the most difficult part of playing a violin or cello. The bow is the instrument’s voice, and all else is subservient. To be sure, it takes years to develop the fine motor control needed to place your fingers at exactly the right place on the fingerboard - being off by just a few millimeters can make a note seriously out of tune. But controlling the bow is even more difficult. It’s similar for blown instruments such as the saxophone and oboe. After a year or two a dedicated student can learn to map notes on the printed page to the equivalent key fingers automatically without thinking. But developing the necessary breath and mouth control is much more difficult, taking thousands of practice hours over many years to truly master.
Instrument Types
There are two basic types of musical instruments: percussive instruments, where the sound is started once then dies away on its own as with a piano or cymbal, and sustained instruments where the player has continuous control of the duration, volume, timbre, and vibrato as with a violin or trombone. For example, a violinist may start a note softly using a slow bow speed, then increase the volume by drawing the bow more quickly, then increase the brightness of the note by moving the bow closer to the bridge, finally adding vibrato that gradually becomes faster. These variations over time make music more expressive, and thus more interesting to hear.
Percussive instruments can also be played in an expressive sustaining fashion, such as a roll on a snare or timpani drum, where the drum is struck repeatedly. A drum roll can also change tone quality over time, by varying how hard you strike the drum and where, as well as the speed of the roll’s repetition. Likewise, mandolin players create a sustained tremolo by repeatedly picking the same note quickly, to continue the note indefinitely. But to my way of thinking, instruments fall into these two basic categories - percussive and sustaining.
Besides controlling the tone with playing technique, another factor that affects an instrument’s timbre as heard by an audience or microphone is its directivity. As with loudspeakers, the vibrating wooden plates of a violin radiate more directionally at high frequencies. Below about 400 Hz violins radiate almost omnidirectionally, but by 4 or 5 KHz almost all of the sound goes upward in a narrow beam, with very little energy sent forward. Reed instruments such as the clarinet and saxophone also radiate in different directions at different frequencies, as well as from different parts of the instrument depending on which keys are pressed. In a concert hall, the full spectrum of sound reaches the audience in large part via reflections from the stage wall behind the performers, and the flared ceiling and angled side walls.
Earlier chapters explained that an FFT analyzer can display the amount of energy at different frequencies in a recording, and this tool can also analyze the output of musical instruments. Understanding the spectrum of instruments helps one to be a better synthesizer programmer, mixing engineer, orchestra arranger, or just a more knowledgeable and appreciative listener. For example, an electric bass often has less energy at the fundamental frequency than the first few harmonics, depending on where along its length the string is plucked. Much of the fullness of bass instruments is determined by the level of the second harmonic, so bringing that out with EQ can make a mix sound solid without relying on very low frequencies that are difficult for many loudspeakers to reproduce at loud volumes.
Figure 1 shows the spectrum of my Fender Precision electric bass playing a low A note, when plucked with a finger directly over the pickup. You can see that the second and third harmonic components are louder than the fundamental. However, plucking the string farther from the bridge, closer to the center of the string, creates a mellower tone having more fundamental with softer harmonics. Plucking a string with less force also reduces harmonic content.
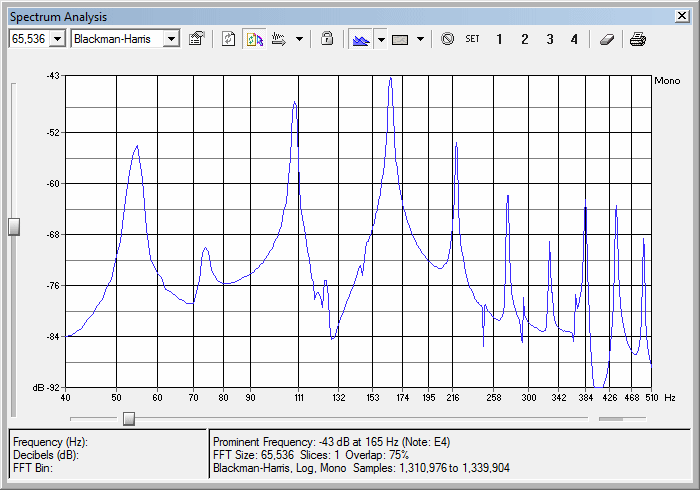
Figure 1: Depending on where you pluck a string, and how hard, the fundamental frequency may be softer than some of the harmonics. This FFT shows the spectrum of a low A note on a Fender Precision Bass when plucked with a finger, with no EQ applied. You can see the second harmonic at 110 Hz is about 7 dB louder than the fundamental at 55 Hz, and the third harmonic at 165 Hz is about 3 dB louder than the second harmonic.
Figure 2 shows an FFT of the same low A note recorded from a Yamaha grand piano. Again, the fundamental is softer than the second harmonic, which in turn is softer than the third harmonic. However, a piano is brighter sounding than an electric bass played with fingers (as opposed to a pick), and this is reflected in the higher harmonics falling off in level much less quickly than an electric bass. 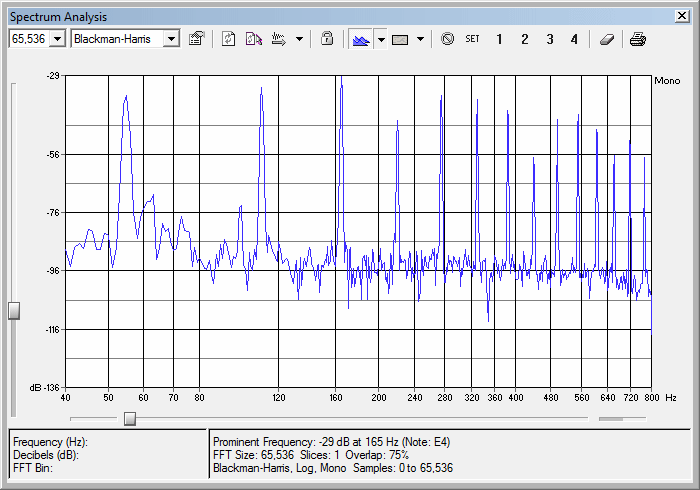
Figure 2: Low notes on a piano often have less energy at the fundamental pitch than the first few harmonics, though the higher harmonics fall off less rapidly than an electric bass.
The Harmonic Series is Out of Tune
Vibrating strings on a violin or guitar, and vibrating air in woodwind and brass instruments, create harmonics, also called overtones, that follow a specific mathematical series. The lowest frequency is the fundamental, and each harmonic is a whole number multiple of that frequency. Harmonics of static waves such as sawtooth and pulse also follow the same series. Table 1 shows the harmonic series of a low A note whose fundamental pitch is 55 Hz, and each harmonic is 55 Hz higher than the previous one.
| Harmonic | Frequency | Nearest Note | Nearest Note Frequency | Error |
|---|---|---|---|---|
| A Fundamental | 55 Hz | A | 55.0 Hz | 0.0% |
| 2nd Harmonic | 110 Hz | A | 110.0 Hz | 0.0% |
| 3rd Harmonic | 165 Hz | E | 164.8 Hz | 0.12% |
| 4th Harmonic | 220 Hz | A | 220.0 Hz | 0.0% |
| 5th Harmonic | 275 Hz | C# | 277.2 Hz | 0.8% |
| 6th Harmonic | 330 Hz | E | 329.6 Hz | 0.1% |
| 7th Harmonic | 385 Hz | G | 392.0 Hz | 1.8% |
| 8th Harmonic | 440 Hz | A | 440.0 Hz | 0.0% |
| 9th Harmonic | 495 Hz | B | 493.9 Hz | 0.2% |
| 10th Harmonic | 550 Hz | A | 550.0 Hz | 0.0% |
| 11th Harmonic | 605 Hz | D | 587.3 Hz | 3.0% |
| 12th Harmonic | 660 Hz | E | 659.3 Hz | 0.1% |
| 13th Harmonic | 715 Hz | F | 698.5 Hz | 2.3% |
| 14th Harmonic | 770 Hz | G | 784.0 Hz | 1.8% |
Table 1: The harmonic series of most musical instruments follows this same basic sequence, becoming out of tune at some higher frequencies. This table shows the first 15 frequencies produced by a low A note, and you can see that the pitch of the fifth harmonic is off by nearly one percent. At the 11th harmonic, which can be audible on a bright sounding instrument playing a low note, the frequency is off by three percent. The musical distance between two adjacent notes is about six percent, so three percent is seriously out of tune!
Harmonics usually become softer as they go higher, so a single note doesn’t necessarily sound out of tune with itself. Even though the 11th harmonic is off by three percent, which at half of one musical interval is a lot, on this particular piano and microphone placement it’s 11 dB softer than the fundamental. It’s also partially masked by all the other harmonics that are in tune.
The available fundamental notes on brass instruments also follow the harmonic series shown in Table 1. Consider the bugle, which is similar to a trumpet, but with no valves to vary the tube length. Bugles can play only notes in the harmonic series, which the player selects by adjusting the shape of his mouth and lips, collectively known as the embouchure. There are many well known “standards” in the bugle literature, such as Taps and Reveille. All bugle tunes contain only the same limited range of notes - basically the chord tones of a major key. As a bugle plays higher notes, the fundamental pitches are inherently out of tune, requiring the player to adjust his embouchure, and blow harder or softer to force the correct pitch. When a player adjusts a note’s pitch this way, he is said to lip the note.
As an aside, a single note played on a guitar can sound out of tune if the strings are old. Strings often stretch non-uniformly, creating one or more thinner portions. Depending on where the thin spots occur along the string’s length, some of the prominent lower harmonics can sound out of tune with the fundamental. It’s very difficult to tune a guitar with old strings!
As used here, the term “harmonic” refers to the natural overtone series of a vibrating string, or the vibrating air column in a wind instrument. Another type of harmonic is created artificially with string instruments by placing a finger lightly on the string at specific locations while plucking or bowing. Touching a string lightly at a point halfway along its length creates a note one octave higher than the open string. Pressing the string firmly against the fingerboard creates a note having the usual overtones, but this type of harmonic is closer to a pure sine wave. Other locations along the neck do the same - common locations are 1/3rd and 1/4th the length, but other integer divisions also work. In fact, doing this at 1/7th the neck’s length creates the same out of tune musical 7th (plus two octaves) as the overtone that occurs naturally within a single note.
Equal Temperament
Equal temperament is a method of tuning that uses a fixed interval between adjacent notes, rather than follow the naturally occurring harmonic series. Equal temperament divides an octave into twelve equally spaced intervals, called musical half-steps. The exact ratio between any note and the next higher note is 1.0595 to 1, where 1.0595 is the 12th root of 2. The frets on a guitar neck are arranged in this ratio, and all modern instrument tuning meters use this method to show if the pitch is too high or too low.
Hundreds of years ago brass instruments had no valves. Like a bugle, early horns and trumpets could produce only a limited number of specific notes. Even though an F horn with no valves can play a high C, that note is out of tune making the horn unsuitable for playing music in the key of C. So players either had to own several instruments, each designed to play in a different key, or they’d insert replaceable crooks - short sections of pipe - to vary the overall length of the tubing. Changing crooks during a performance takes time, so valves were added to trumpets and French horns around 1815. This also allowed musicians to play notes in the equal-tempered scale rather than only notes in the harmonic series.
The concept of equal temperament goes back thousands of years, but J.S. Bach championed it and made it a modern reality. His 1722 The Well-Tempered Clavier is a series of 24 pieces - one in each major and minor key - written for the keyboard instruments of his day. This had great musical as well as technical impact, because it allowed musical compositions to modulate to distant keys without some instruments sounding out of tune.
Another tuning method called just intonation tunes the fifths to exact harmonic frequencies. In that case, the lowest E note in Table 1 would be tuned to 165 Hz instead of 164.8 Hz. String players often tune their instruments this way by playing adjacent open strings while listening for beat tones - a slow volume undulation as two notes approach perfect unison. You play both notes at once, and adjust the tuning of one until the pulsing slows to a stop. There’s no difference between playing two notes at once having slightly different pitches, or one note that’s amplitude-modulated by a slow tremolo effect. The resulting sound, waveform, and spectrum are identical.
Another tuning technique uses harmonics to achieve a perfect unison. Touching a guitar A string lightly at the seventh fret creates an E note an octave and a half higher than the open string. Lightly touching the E string below the A at its fifth fret creates the same E note. So you can play both harmonics, one after the other letting both continue to ring, and tune either string until the beating slows to a stop. Tuning via harmonics is especially useful for basses, because our pitch perception is poor at low frequencies.
Many musicians intentionally play notes ever-so-slightly sharp or flat for expression or effect. If not for the note’s entire duration, they may slide up to a note from a lower pitch. Playing a note slightly flat can project a sense of calm, and playing slightly sharp adds tension. Again, I’m talking about extremely small amounts, on the order of five or ten cents - 1/100ths of a musical half-step. Playing off-pitch intentionally is easy with fretless instruments such as the violin or cello, and wind instrument players do that by varying their embouchure. Guitar players change the pitch in large or small amounts by bending the strings, which is one reason their strings can stretch non-uniformly as mentioned earlier. Musicians can also play slightly behind the beat, or a little ahead - say, 10 to 30 milliseconds - to add a sense of calm or tension.
“Wood Box” Instruments

As with listening rooms, instruments made from a hollow wooden “box” of some type also have resonant modes whose frequencies are related to the box dimensions. To avoid having modal resonances make some notes much louder than others, violins, guitars, and other wood box instruments are designed with an irregular curved shape. These instruments still have modes, but the continuous curves along the sides minimize a strong build-up at single frequencies and their multiples.
Also like rooms, when a resonant mode is near, but not exactly at, a frequency being played, the result is an out of tune beat frequency caused by the frequency difference. This produces an effect known as a wolf tone, and it’s more prominent in cellos and acoustic basses than smaller wood box instruments. In many cellos, a strong resonance occurs somewhere between the E at 164.8 Hz and the F# at 185 Hz. Whether or not the resonance is exactly in tune with a standard note frequency, that one note will sound louder than the others, and be more difficult for the player to control with the bow. Even very good cellos can have wolf tones, and various devices that attach to the cello body or a low string are available to reduce the effect.
Wood box instruments also have one or more holes in the front plate to allow lower frequencies to escape. Acoustic guitars typically have a single round hole about four inches in diameter, and instruments in the violin family have two holes shaped like a lowercase italic “f” called, appropriately, F holes. All wood box instruments create sound using the same basic principle as the cello shown in Figure 3. Four or more strings are stretched tightly above the fingerboard, with both ends anchored solidly by the tuning pegs and tail piece. The active vibrating length of the strings is between the nut at one end by the tuning pegs, and the bridge that rests on the body. These also hold the strings in place side to side. The same names are used for related pieces on acoustic guitars and banjos, though on those instruments the bridge and tail piece are a single unit called a saddle. The cello mute shown here is a small block of rubber that’s placed onto the bridge to partially damp its vibration